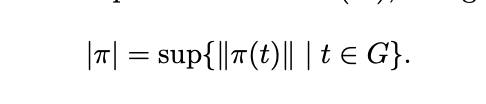In theorem 1.1 (see below) Pisier shows that a quantitative condition on the invertible operator which unitarizes a uniformly bounded implies the amenability of the group.

where

Is there a known example of an amenable group which has a uniformly bounded representation pi which is unitarizable where ||S|| ||S^-1|| > |pi|^2?